Test Results: The Middle-Square Weyl Sequence PRNG



Implementation

In 2017 Bernard Widynski published a paper suggesting a way to improve on the original Middle Square Method. His solution was to incorporate a Weyl Sequence into the middle of the steps. This added two new variables, w and s, which resulted in a longer period and greatly increased randomness of the generator.

The variable w acts as a counter, increasing each iteration by s. s itself is a constant; in Widynski's paper, it was given the value $B5AD4ECEDA1CE2A9, so that's what this study uses in its implementation.

This altered version of the Middle Square Method uses the following steps:
  1. Add s to the current value of w.
  2. Add w to the square of the current Seed.
  3. Pad the resulting number with 0s until it is n*2 digits long.
  4. Take the middle n digits. This is both the new Seed and the returned random number.


As before, we will use 4 as the value of n. This limits the generator to a range of 0 to 9999, inclusive, but the addition of the Weyl Sequence will help prevent this generator from falling into a loop or returning as many repeated values.


Test Results

Period Length Test
SEEDNumber indicates how many results could be obtained before the generator fell into a loop.
1138-PASS
65535-PASS
8675309-PASS
16777216-PASS
123456789-PASS


Dice Roll Test
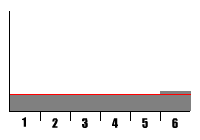Adding a Weyl Sequence made this generator's output nice and evenly distributed.


Dartboard Test
SEEDMinimum of 6,000 darts placed needed to pass.
11383706FAIL
655353690FAIL
86753093708FAIL
167772163676FAIL
1234567893732FAIL


Crush Test
SEED70% or higher required to pass.
1138101%PASS
65535101%PASS
8675309101%PASS
16777216101%PASS
123456789101%PASS


Plot Test
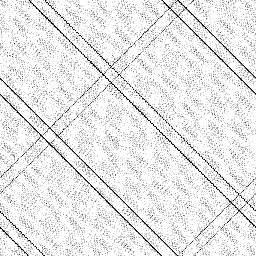As you can see, this is a huge improvement over the Middle Square Method. However, the stripes indicate that there's a clear pattern to the randomness, which means this generator fails the plot test.


Example Output
79414761831759476064451639608406714427064199134468443288796667222689228666421
4905935126202918736488182374537782388572339078364771832758507037452538638309724
427963229231478433587816677232679428756431480792542629282172678828238452807265
85823293773947818336575280104535376582127344289622593284884238868466862426697
28856441471091562639272371698838239351836292859231967642479183465655898345453668
81147434299612794254974140858766962526600289564504613905926492626707288482403
508553198602309875454800835655589956455435718017753430960309523507404384896706
26165022905646045168962265925296975885724134988434686113001744748108365546092
45643473792076343185933962051739468392671627164052914647044188864266824316878
88672422489133738621290473504820837553631904574337678227734328583597175273849
8295672528163082924647943218767267823346780887724324793240086312806725348308385
5266287458432797725782433857389815536375181976735290621129346489422486702688
223766838887244246961427864127097155483983955168384459331827628792434756419912
54636548100674530061132944649941268573269821396586889624524599454865026127058
4849840450714824603308475308024357554495563557800367553106016295365094029
847527072042648889062461450194818660251569614859841449745794613298774338124367
54461075663459790667643205919296365183932837827171945639189162471440485088670
241768634868842448776764623289073368214377534920457533627808677432958212973
6528383482812727184862948925248143077535868023206766487884344779774463227927239
8314386525230158532657711678433957242982653837378183273617506196893524914210


A WFTID Website