Test Results: The Middle-Square Method PRNG



Implementation

The Middle Square Method is a very simple, and very low quality, pseudo random number generator.

This generator works via a short series of steps:
  1. Take the current Seed and square it.
  2. Pad the resulting number with 0s until it is n*2 digits long.
  3. Take the middle n digits. This is both the new Seed and the returned random number.


Its creator, Br. Edwin, suggested that n should be 4. That is the value used by this study, and this limits the generator to a range of 0 to 9999, inclusive. Changing the value of n will greatly alter the generator's possible range and the likelihood of the generator falling into a loop. As it is, an n value of 4 traps the generator in loops remarkably quickly, making it useable only as an example.


Test Results

Period Length Test
SEEDNumber indicates how many results could be obtained before the generator fell into a loop.
113830FAIL
6553535FAIL
867530926FAIL
1677721612FAIL
12345678918FAIL


Dice Roll Test
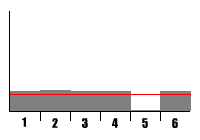While this PRNG's very limited period causes it to fall into repeating patterns, its output is surprisingly well distributed, even if you consider that almost no 5s appeared.


Dartboard Test
SEEDMinimum of 6,000 darts placed needed to pass.
113815FAIL
6553517FAIL
867530913FAIL
167772166FAIL
1234567899FAIL


Crush Test
SEED70% or higher required to pass.
11381%FAIL
655351%FAIL
86753091%FAIL
167772161%FAIL
1234567891%FAIL


Plot Test
Thanks to its very small period, this PRNG wasn't able to plot many points, and so fails the plot test by a large margin.


Example Output
26098068926857451343579809248047846146773379928720384147417269790844125042700
29004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100
21004100810061002100410081006100210041008100610021004100810061002100410081006100


A WFTID Website