Test Results: Borland's lrand()



Implementation

Borland was once a very well known company in tech circles; their Turbo Pascal and C/C++ compilers were quite famous. Their compilers also came with distinctive controls, so you could always tell when software was developed using their tools. While they are no longer in business, they did leave a legacy behind.

In this case, their C/C++ compiler provided two Linear Congruential Generators, each of which also featured a slight twist - they used a bit mask to return only a portion of the Seed value. This page is specifically for their lrand function, which returns only the last 30 bits of the Seed.

lrand uses the following constants in its generator:


Test Results

Period Length Test
SEEDNumber indicates how many results could be obtained before the generator fell into a loop.
1138-PASS
65535-PASS
8675309-PASS
16777216-PASS
123456789-PASS


Dice Roll Test
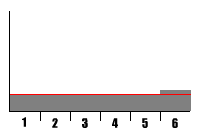This generator produced an ideal distribution of outcomes.


Dartboard Test
SEEDMinimum of 6,000 darts placed needed to pass.
11386969PASS
655357014PASS
86753096971PASS
167772166966PASS
1234567897003PASS


Crush Test
SEED70% or higher required to pass.
1138101%PASS
65535101%PASS
8675309101%PASS
16777216101%PASS
123456789101%PASS


Plot Test
An ideal result for this test.


Example Output
38518584678410943226034322586915499479838219327384412161803906474758078365033677541316625759361973877317169410693193238913785576735121301979472993102489427707554283479351021068758
448942571924251462677006929947261833495722756813114822608978349770080326642361239561672668549268989326643395434357539880389340309260702788606969798171030508687569587762800737878734
72411481024354480019752924156458815268529619610592116636964861328762419872279246816936143111017548888845531193954151695732243545672110613529936899738861062630442901395735504267529
146420873703353910067608846584927522567746592158789146618656291070710261011255436113059732100641836412708607478034579128133161321888075128181270171808830666387634935400019603984960
43189825746470144112201510512030308959591845215467295288235188115506533251893303210233037858266792258345515424908463848566876082894420067742004212945779726962029526170574431065906363
386020442826966695104800514680113948413119644333247561192024217110710730671210520034785831281661372989491773744944834512747929650236280814467441663648747576390159347560992741148168
8581003750007726315540289756971586541859370594665925783077474920940301256341688617675419365605347968089294632860878015707207028008737306108201192029759035144745781474406218435
9908616515737394591053564150384303142565023998100639395391465699215063324531304027590255478461907237560186745901191206395607448543114079150829557764043136708442974638971135567070037
73616639018671691971398002204534323417392833573032971010165710819505191626055570745382830339090058179396678561272730105222608313700110706756463142142692102930013146542720688786483
950463292201461984051381297403357491436743167961424957787653227729067042403235707170369147808356348554042171470560569547851838802159683989675099762008661914542103563385135691960
20457873083034083659435520714106217442101984350750217484192178824021884274190809983484373308629769634860976963856533124784631006732261648310060657362480960500153352064659895210153
107122659920186270775206861450790703966835635536772589237780965191349055132040428045769648573984397461038018562803969618145290641637084210876224748843474312233692267236721878974639
23259622239822834758125766358539923278234107513125186660502280269326352103376101730719747573725778788584379010326938611331492913477941188453404514007044645710979498010059045388469
4936167283526300650605134722879441125349962368227314862084754772609415518280591463340493152777107013714249466131119899304112367232547875573341902701021932781127491700912553276
316464464293288477910577891102772923877193737779791128326923426557695904990578575859274911243635403744987718669911231321062924640899137653790526142004343889868539329039427942595469
45377031957310024111270639391059213339135418990218747638433792882351478661116774756314111779802773133768300163251378411152240871350200742999270506089430189824823261020672398828461
4673970149966445148711218818237740578514402478667734038735634068777129417946628591009488913465543189105360701335909396397490574052014079010085448122918639999052731909704332747217960
12955306558085540132897541185297477180487612994263107889417716313094154720223100957408416934256835310139684655032577190391503543651498906381065460345738381827947878485488561731
57107768050957023940324535142990340873909134644384486771945469425766421868793811020351641075877132645483812448171614286700858640324592313197338710752553792795257838387683247316228
163106009800979842869859260105969440847936028022505124545547553810244496394914686743647135716846576084282540147616297643183119092439894498673425558943370734419626222219716996140026


A WFTID Website